非晶固体中的两步力学行为转变
在物理学的广阔领域中,物质状态的变化一直是一个引人入胜的研究课题。我们对晶体熔化的理解已经相对成熟:在三维空间中,晶体通过一级相变熔化为液体;而在二维空间中,固体通常会经历一个两步熔化过程(KTHNY理论),即从固态到中间态(hexatic phase),再到液态。然而,关于非晶固体与液态之间的转变,一直是物理学领域中一个尚未完全解开的谜团。
近期,中国科学院理论物理研究所金瑜亮研究团队与物理研究所的博士后付洋(理论物理所2023届博士研究生),以及魏茨曼科学研究所的Itamar Procaccia合作,基于分子动力学模拟及理论分析,研究了可以忽略热涨落的二维无摩擦无序颗粒材料,通过对中心粒子的均匀膨胀的瞬时扰动的位移响应分析,揭示了非晶材料在解压熔化中的固液两步转变:首先是固相内的弹性-塑性转变,随后是塑性行为主导的固相到液相的非阻塞转变。这一研究以《Long-Range Angular Correlations of Particle Displacements at a Plastic-to-Elastic Transition in Jammed Amorphous Solids》为题,发表在最新一期的物理评论快报上(Phys. Rev. Lett. 134 (2025),178201)[1],见链接https://journals.aps.org/prl/abstract/10.1103/PhysRevLett.134.178201。
研究团队构建了一个二维双分散系统,其中的纯排斥势圆盘,位于固定圆形外边界和瞬时膨胀内边界之间。研究发现,当系统处于比较高的压强时,中心粒子均匀膨胀所产生的位移场的径向衰减形式(见图(1h,k)),可以由经典线性弹性理论所描述;当系统压强降低到某一临界值后,位移场的塑性特征愈发明显,甚至会出现一种反直觉的现象——大量粒子在感受到内边界粒子的膨胀后反而朝中心粒子运动(该行为可以被Itamar等人建立的力学响应屏蔽理论所描述[2])(见图(1d,e)),并会出现角向位移关联函数的急剧衰减;而当继续降低压强使体系处于非阻塞态时,中心粒子膨胀所影响的范围(见图(1a,b),位移几乎衰减到0的距离可定义为径向关联长度)随非阻塞程度呈现幂律衰减,其幂律指数与之前文献中结果一致[3]。经过进一步研究发现,在塑性-弹性转变压强附近,新定义的描述位移角向关联的长度/角度尺度表现出了幂律发散的行为,这表明系统中存在长程的角向关联。这种角向关联的出现,为理解非晶材料的力学行为转变提供了一个全新的视角。更进一步地,该研究还探讨了系统尺寸、颗粒间相互作用形式、及中心粒子膨胀程度对转变的影响,从而确认了这一发现的普适性,并基于标度论证及模拟数据结果建立了弹塑性转变的普适标度形式。
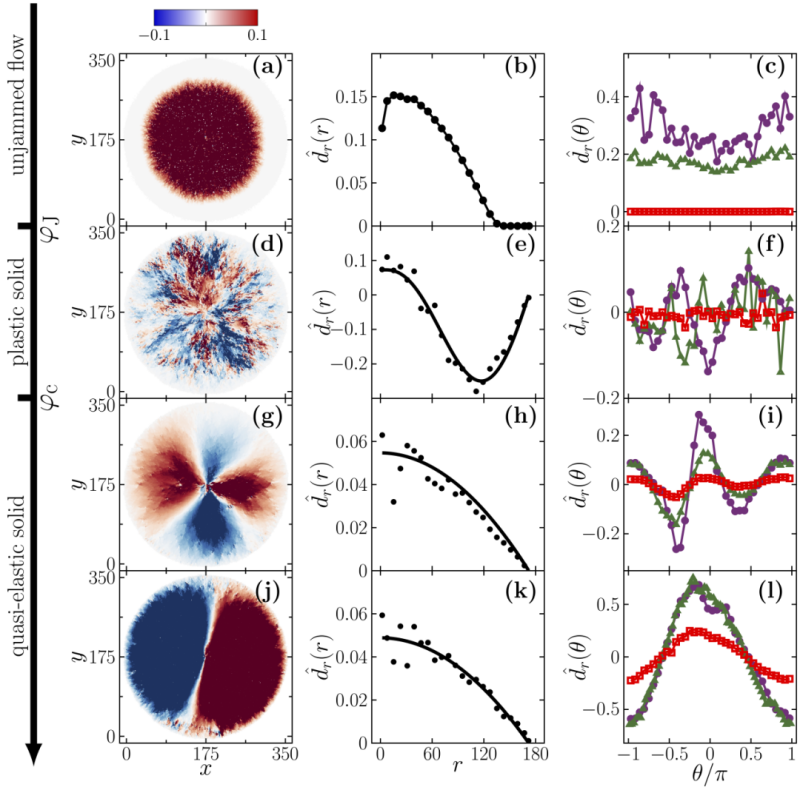
图1:对于中心粒子瞬时膨胀体系,圆形边界内的粒子在力学平衡前后的径向位移场。各子图展示了不同压强条件下的典型力学响应行为,压强自上而下从零呈递增趋势。 第一列:使用最大值进行归一化后的径向位移场的热图; 第二列,角平均后的,其中后三副图中的实线为基于力学响应屏蔽理论的解析解所拟合的结果; 第三列,在三个不同环形区域内的粒子在不同角度上的径向位移(分别是紫线、绿线、和红线)。
除了非晶固体对于点源微扰的径向位移响应的反常振荡现象之外,该研究所揭示的两步解压熔化的物理图像,与Itamar研究团队建立的力学响应屏蔽理论的预测同样一致[2]。该理论指出,塑性响应具有准局域化的四极子结构特征,(准)弹性-塑性-非阻塞转变,可以从四极屏蔽-偶极屏蔽-单极屏蔽来理解,这与著名的KTHNY相变中的固相-六角相-液相的转变有相似之处。然而,前一种转变更加普适,因为它不受维度的限制[4]。

正文链接:
https://journals.aps.org/prl/abstract/10.1103/PhysRevLett.134.178201


